5.5 Curvatures of Minimal Surface
When a minimal surface $r(u,v) = (x(u,v),y(u,v),z(u,v))$ is represented by an isothermal coordinate system, we define $\phi_1(w), \phi_2(w), \phi_3(w), f(w)$ and a meromorphic function $g(w)$ as:
$$ \phi_1(w) = \frac{\partial x}{\partial u} - i \frac{\partial x}{\partial v}, \quad \phi_2(w) = \frac{\partial y}{\partial u} - i \frac{\partial y}{\partial v}, \quad \phi_3(w) = \frac{\partial z}{\partial u} - i \frac{\partial z}{\partial v}, \quad f = \phi_1 - i\phi_2, \quad g = \frac{\phi_3}{\phi_1 - i\phi_2} $$
Hence:
$$ r_u = \frac{1}{2}(\phi_1 + \overline{\phi_1}, \phi_2 + \overline{\phi_2}, \phi_3 + \overline{\phi_3}), \quad r_v = \frac{i}{2}(\phi_1 - \overline{\phi_1}, \phi_2 - \overline{\phi_2}, \phi_3 - \overline{\phi_3}) $$
$$ r_u \times r_v = \frac{|f|^2 (1 + |g|^2)}{4}(2Re(g), 2Im(g), |g|^2 - 1) $$
Thus, a unit normal vector $e$ is given by:
$$ e = \frac{r_u \times r_v}{|r_u \times r_v|} $$
The first fundamental form is:
$$ I = \frac{1}{2} \left( |\phi_1|^2 + |\phi_2|^2 + |\phi_3|^2 \right) dw d\overline{w} $$
By
$$ \begin{aligned} &\frac{\partial}{\partial w} = \frac{1}{2}\left( \frac{\partial}{\partial x} - \frac{1}{i} \frac{\partial}{\partial y} \right), \quad \frac{\partial}{\partial \overline{w}} = \frac{1}{2}\left( \frac{\partial}{\partial x} + \frac{1}{i} \frac{\partial}{\partial y} \right), \end{aligned} $$
We obtain:
$$ \begin{aligned} r_{uu} &= \frac{1}{2}(\phi_1’ + \overline{\phi_1’}, \phi_2’ + \overline{\phi_2’}, \phi_3’ + \overline{\phi_3’}), \ r_{uv} &= \frac{i}{2}(\phi_1’ - \overline{\phi_1’}, \phi_2’ - \overline{\phi_2’}, \phi_3’ - \overline{\phi_3’}), \ r_{vv} &= -\frac{1}{2}(\phi_1’ + \overline{\phi_1’}, \phi_2’ + \overline{\phi_2’}, \phi_3’ + \overline{\phi_3’}). \end{aligned} $$
Then calculating $L, M, N$, we get:
$$ L = -N = Re(f g’), \quad M = Im(f g’) $$
Hence, the second fundamental form is given by:
$$ II = -Re\left( f \frac{dg}{dw} dw^2 \right) $$
We calculate the Gaussian curvature $K$ and obtain principal curvatures $\kappa_1, \kappa_2$ by $H = 0$:
$$ \kappa_1 = \frac{4|g’|}{|f|(|g’|^2 + 1)^2}, \quad \kappa_2 = -\frac{4|g’|}{|f|(|g’|^2 + 1)^2}, \quad K = -\left( \frac{4|g’|}{|f|(|g’|^2 + 1)^2} \right)^2 $$
Visualization of Minimal Surface
As we conclude our exploration, we’ve delved deep into four fascinating minimal surfaces: the catenoid, helicoid, Enneper’s surface, and Scherk’s surface. These minimal surfaces not only showcase the beauty and depth of mathematics but also play crucial roles in the natural world and scientific research. Now, through visualization, let’s revisit the key features and geometric properties of these surfaces. This will be an exciting recap, helping you better understand and appreciate these mesmerizing mathematical structures.
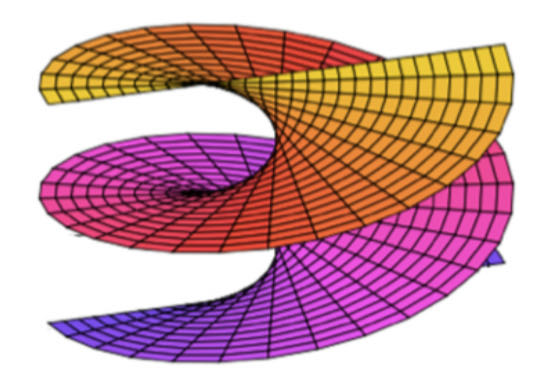
Example (Helicoid)
$$ f = -ie^{-iw}, \quad g = ie^{iw}, \quad w \in \mathbb{C} $$
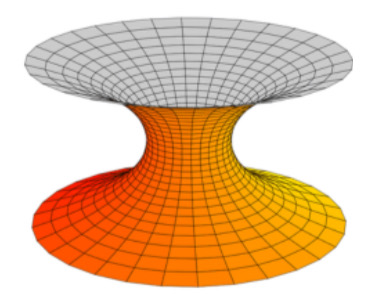
Example (Catenoid)
$$ f = -ie^{-iw}, \quad g = e^{iw}, \quad w \in \mathbb{C} $$
Example (Enneper’s Surface)

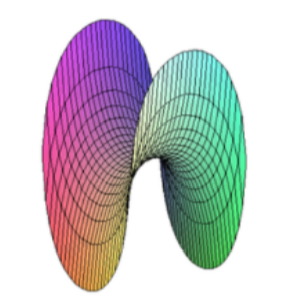
Example (Scherk’s Surface)