In this section, we use the calculus of variations to find the equations of minimal surfaces, and before we begin, we need to understand what a calculus of variations is. For ease of understanding, the variational will be introduced in more general terms.
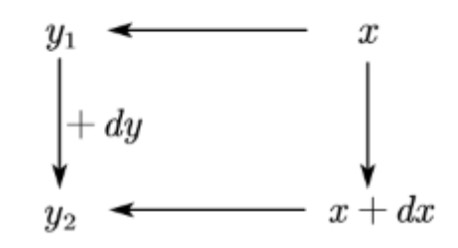
Before we start to introduce calculus of variation, we need to recall what is differentiation. Suppose $f(x) : D \to \mathbb{R}$ be a continuous and differentiable function, When the independent variable $x$ undergoes a very small change $dx$, it is not difficult to see that the function value also changes due to the change in the independent variable; this is called differentiation of the function.
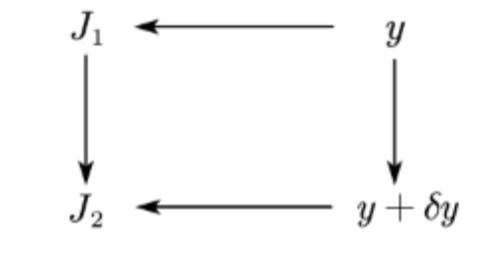
Variation is similar to differentiation in that it extends functions to functional, and when a function $y$ undergoes a very small deformation $\delta y$, its functional also changes due to the deformation of $y$ and a change in $\delta J$.
In the following we study the equations of the minimal surface.
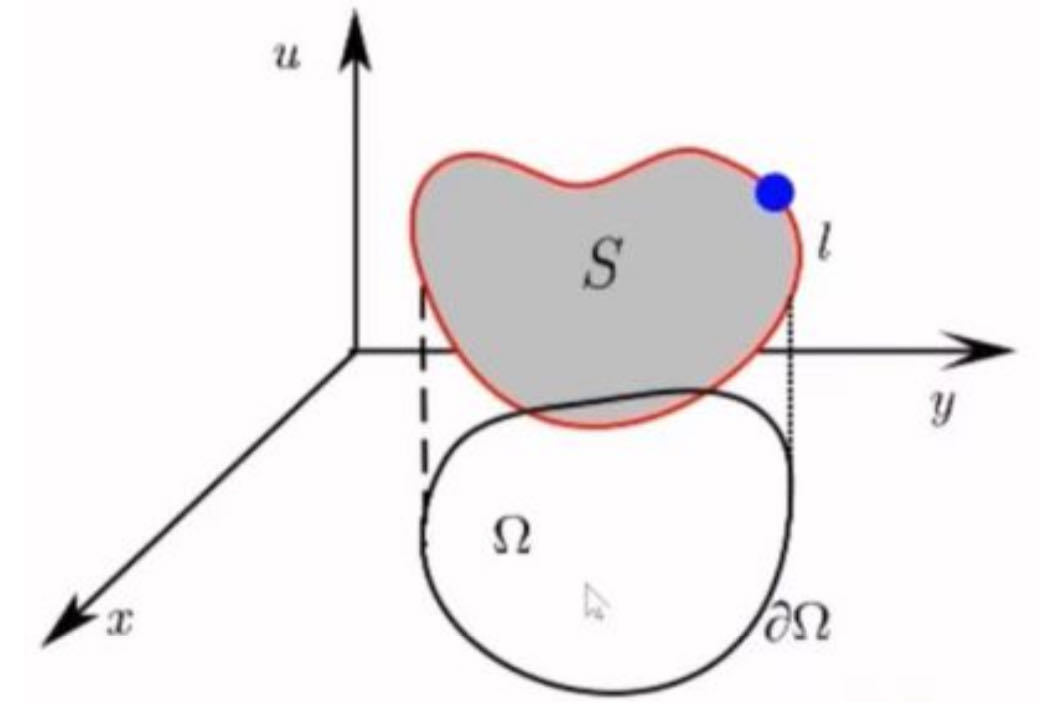
As shown in the figure, $\Omega$ is a closed curve in the $xOy$ plane bounded by $\partial \Omega$. Our task is to find a surface $S$ defined on $\bar{\Omega}$ such that $S$ is bounded by $l : x = x(s), y = y(s), u = \phi(s)$ and the surface area of $S$ is minimised.
Given a set of functions
$$M_\phi = { v \mid v \in C^1(\bar{\Omega}),v|_{\partial \Omega} = \phi }$$
then define functional $J : M_\phi \to \mathbb{R}$ on $M_\phi$
$$J(v) =\iint_\Omega\sqrt{1+ v_x^2 + v_y^2} , dx , dy.$$
It is known as the formula of integral of area of surface. Now we need to find $u \in M_\phi$, which leads to
$$J(u) = \min_{v \in M_\phi} J(v)$$
Define
$$M_0 = { v \mid v \in C^1(\bar{\Omega}),v|_{\partial \Omega} = 0 }$$
Then for any $v \in M_0$, $\epsilon \in (-\infty, \infty)$, $u + \epsilon v \in M_\phi$. Define a differentiable function $j : \mathbb{R} \to \mathbb{R}$ as:
$$ j(\epsilon) = J(u + \epsilon v). $$
Since $j(\epsilon) \geq j(0)$ for all $\epsilon \in \mathbb{R}$, it follows that:
$$ j’(0) = 0. $$
By calculating we get:
$$ j’(\epsilon) = \iint_\Omega \frac{(u + \epsilon v)_x v_x + (u + \epsilon v)_y v_y}{\sqrt{1 + (u_x + \epsilon v_x)^2 + (u_y + \epsilon v_y)^2}} , dx , dy. $$
Let $\epsilon = 0$, we obtain:
$$ \iint_\Omega \frac{u_x}{\sqrt{1 + u_x^2 + u_y^2}} v_x + \frac{u_y}{\sqrt{1 + u_x^2 + u_y^2}} v_y , dx , dy = 0. $$
Suppose $u \in C^2(\bar{\Omega})$, let:
$$ P = \frac{u_x}{\sqrt{1 + u_x^2 + u_y^2}}, \quad Q = \frac{u_y}{\sqrt{1 + u_x^2 + u_y^2}}. $$
By Green’s theorem:
$$ \iint_\Omega \left( \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} \right) dx , dy = \oint_{\partial \Omega} \left(P \cos(n, x) + Q \cos(n, y)\right) dS. $$
Since $v|_{\partial \Omega} = 0$, we derive:
$$ \frac{\partial}{\partial x} \left( \frac{u_x}{\sqrt{1 + u_x^2 + u_y^2}} \right) + \frac{\partial}{\partial y} \left( \frac{u_y}{\sqrt{1 + u_x^2 + u_y^2}} \right) = 0. $$
Simplifying, we obtain the minimal surface equation:
$$ u_{xx}(1 + u_y^2) - 2u_x u_y u_{xy} + u_{yy}(1 + u_x^2) = 0. $$